Vorschlag: Verwendung des STAR VOTING Verfahrens: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 7: | Zeile 7: | ||
* Die Kandidaten M1 und M2 in der Mitte orientiert sind und auch sehr beliebt sind | * Die Kandidaten M1 und M2 in der Mitte orientiert sind und auch sehr beliebt sind | ||
* Kandidat R rechts orientiert ist und auch nicht sehr beliebt ist. | * Kandidat R rechts orientiert ist und auch nicht sehr beliebt ist. | ||
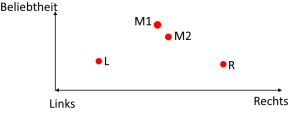
[[Datei:LinksRechtsBeliebtheit.png|mini|Abbildung 1: Kandidaten nach Beliebtheit und politischer | [[Datei:LinksRechtsBeliebtheit.png|mini|Abbildung 1: Kandidaten nach Beliebtheit und politischer Ausrichtung]] | ||
Diese Annahmen sind grafisch in Abbildung 1 dargestellt. Bei der Wahl verteilen sich die Stimmen nun auf die einzelnen Wähler. Bei den beiden in der Mitte orientierten Kandidaten teilen sich die Stimmen der Wahler auf, da sie sehr ähnlich positioniert sind. Zudem wählen auch viele in der Mitte orientierten Personen den linken und rechten Kandidaten, da diese nicht sehr extrem weit links oder rechts positioniert sind. Im Ergebnis reduziert sich die Stimmenanzahl von M1 und M2 soweit, dass sie nicht die ersten beiden Ränge für die nachfolgende Stichwahl erreichen. Die unbeliebten Kandidaten L und R gehen also in die Stichwahl. L oder R gewinnt die Wahl, obwohl diese Kandidaten im direkten Vergleich gegen M1 oder M2 keine Chance gehabt hätten. | Diese Annahmen sind grafisch in Abbildung 1 dargestellt. Bei der Wahl verteilen sich die Stimmen nun auf die einzelnen Wähler. Bei den beiden in der Mitte orientierten Kandidaten teilen sich die Stimmen der Wahler auf, da sie sehr ähnlich positioniert sind. Zudem wählen auch viele in der Mitte orientierten Personen den linken und rechten Kandidaten, da diese nicht sehr extrem weit links oder rechts positioniert sind. Im Ergebnis reduziert sich die Stimmenanzahl von M1 und M2 soweit, dass sie nicht die ersten beiden Ränge für die nachfolgende Stichwahl erreichen. Die unbeliebten Kandidaten L und R gehen also in die Stichwahl. L oder R gewinnt die Wahl, obwohl diese Kandidaten im direkten Vergleich gegen M1 oder M2 keine Chance gehabt hätten. | ||
Diese und ähnliche Entscheidungsprobleme wurden bereits wissenschaftlich untersucht. Das Ergebnis war das sogenannte Arrows Unmöglichkeitstheorem<ref>https://de.wikipedia.org/wiki/Arrow-Theorem</ref>. Das von dem Nobelpreisträger Kenneth Arrow sagt im wesentlichen aus, das es bei rein ordinalen Entscheidungsverfahren (das hier ist so eins), kein faires Entscheidungsergebnis geben kann (bestimmte | Diese und ähnliche Entscheidungsprobleme wurden bereits wissenschaftlich untersucht. Das Ergebnis war das sogenannte Arrows Unmöglichkeitstheorem<ref>https://de.wikipedia.org/wiki/Arrow-Theorem</ref>. Das von dem Nobelpreisträger Kenneth Arrow sagt im wesentlichen aus, das es bei rein ordinalen Entscheidungsverfahren (das hier ist so eins), kein faires Entscheidungsergebnis geben kann (bestimmte Mindestanforderungen für eine gute Entscheidung können nicht erfüllt werden). | ||
=== Beispiel | === Beispiel Bundespräsidentenwahl 2016 === | ||
Um die Praxisrelevanz zu zeigen, wird hier das Ergebnis der Bundespräsidentenwahl 2016 betrachtet. Bei dieser Wahl sind angetreten (mit meinen persönlichen Einschätzungen der Positionierung): | |||
* | |||
== Referenzen == | |||
<references /><!--- ---> | |||
Version vom 11. August 2023, 20:00 Uhr
Das STAR VOTING Verfahren [1] ermöglicht es wesentlich treffsicherer den gewünschten Kandidaten für das Bundespräsidentenamt zu finden als das bisher angewandte Verfahren. Es benötigt darüber hinaus nur einen Wahlgang. Dies spart Kosten für den Staat und Aufwand für die Bevölkerung.
Das Problem des bisherigen Verfahrens
Das derzeitige Verfahren sieht vor das ein Kandidat mehr als die Hälfte aller Stimmen auf sich vereinigen muss. Gelingt das im ersten Wahlgang nicht, so werden die zwei Kandidaten mit den meisten Stimmen nochmals antreten. Im Ergebnis hat dann ein Kandidat mehr als die hälfte aller Stimmen.[2]. Dieses Verfahren ist jedoch nicht gut dafür geeignet den gewünschten Kandidaten zu ermittlen.
Nehmen wir beispielsweise an, dass 4 Kandidaten (L,M1,M2,R) antreten. Nehmen wir weiters an, dass:
- Kandidat L links orientiert ist und nicht sehr beliebt ist
- Die Kandidaten M1 und M2 in der Mitte orientiert sind und auch sehr beliebt sind
- Kandidat R rechts orientiert ist und auch nicht sehr beliebt ist.
Diese Annahmen sind grafisch in Abbildung 1 dargestellt. Bei der Wahl verteilen sich die Stimmen nun auf die einzelnen Wähler. Bei den beiden in der Mitte orientierten Kandidaten teilen sich die Stimmen der Wahler auf, da sie sehr ähnlich positioniert sind. Zudem wählen auch viele in der Mitte orientierten Personen den linken und rechten Kandidaten, da diese nicht sehr extrem weit links oder rechts positioniert sind. Im Ergebnis reduziert sich die Stimmenanzahl von M1 und M2 soweit, dass sie nicht die ersten beiden Ränge für die nachfolgende Stichwahl erreichen. Die unbeliebten Kandidaten L und R gehen also in die Stichwahl. L oder R gewinnt die Wahl, obwohl diese Kandidaten im direkten Vergleich gegen M1 oder M2 keine Chance gehabt hätten.
Diese und ähnliche Entscheidungsprobleme wurden bereits wissenschaftlich untersucht. Das Ergebnis war das sogenannte Arrows Unmöglichkeitstheorem[3]. Das von dem Nobelpreisträger Kenneth Arrow sagt im wesentlichen aus, das es bei rein ordinalen Entscheidungsverfahren (das hier ist so eins), kein faires Entscheidungsergebnis geben kann (bestimmte Mindestanforderungen für eine gute Entscheidung können nicht erfüllt werden).
Beispiel Bundespräsidentenwahl 2016
Um die Praxisrelevanz zu zeigen, wird hier das Ergebnis der Bundespräsidentenwahl 2016 betrachtet. Bei dieser Wahl sind angetreten (mit meinen persönlichen Einschätzungen der Positionierung):
Referenzen
- ↑ https://www.starvoting.org/star
- ↑ Bundespräsidentenwahlrechtsgesetz §17 und §18: https://www.ris.bka.gv.at/GeltendeFassung.wxe?Abfrage=Bundesnormen&Gesetzesnummer=10000494
- ↑ https://de.wikipedia.org/wiki/Arrow-Theorem